Correlation can be confounder determination

Friday November 27, 2020

In a situation of pure confounding (x←z→y) with equivariant noise, the correlation between x and y is the coefficient of determination between z and either x or y: \( r = R^2 \).

I got to thinking about this because of The Book of Why:

"[Burks] computed the direct effect of parental IQ on children's IQ and found that only 35 percent, or about one-third, of IQ variation is inherited. In other words, parents with an IQ fifteen points above average would typically have children five points above average." (page 306)

That works out if we have a simple data-generating model like this in R:

z <- rnorm(1000000, sd=1)            # genetics,            variance=1
x <- z + rnorm(1000000, sd=sqrt(2))  # IQ of parents,  adds variance=2 noise
y <- z + rnorm(1000000, sd=sqrt(2))  # IQ of children, adds variance=2 noise
mean(y[0.9 < x & x < 1.1])
## [1] 0.334556

One third of x and y variance is due to z, and when x values are around 1, average corresponding y value is around 1/3, so that checks out: regression to the mean.

The genetic contribution z isn't really observable, though. All we see are x and y. So how do we get the contribution of z?

Both x and y have variance 3. If we had a twin study in this world, we could recover that variance is 2 when genetics is fixed, and that would let us find that genetics explains 1/3 of variance. But we don't generally have a twin study.

The common thing to do would be a regression.

summary(lm(y ~ x))  # (Pulling out one line of output...)
## Multiple R-squared:  0.1114,     Adjusted R-squared:  0.1114

This is usually interpreted as saying that x explains 11% of the variation of y. That's true enough, but it isn't how much is explained by z.

The correlation between x and y, however, is how much variance is explained by z.

cor(x, y)
## [1] 0.3338363

More generally (for non-equivariant noise) the regression coefficient gives the fraction of variance explained by z. (See also the earlier estimate illustrating regression to the mean.)

So this is a way of estimating the effect of an unobserved confounder, which seems to work in this very simple setting. Is this like what Burks did? Probably her models were not so simple. Is this a special case of some more general approach?

I don't think I've seen this kind of "method" before; I'd love to see more elaboration of this kind of idea for estimating impacts of unobserved variables.

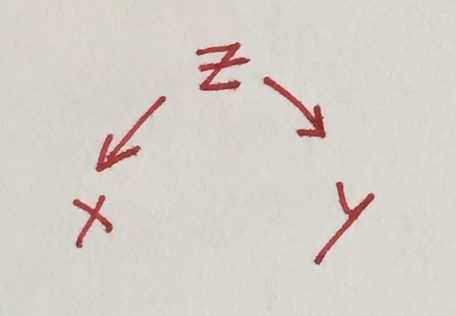
The data-generating model above (and surrounding discussion) requires suspension of disbelief; it represents some sort of asexual reproduction, has additional influences on IQ that are entirely uncorrelated between parents and children, and of course IQ is fraught as a topic to begin with. Hopefully the statistical considerations are still visible.