Dot product really does give you cosine

Saturday September 4, 2021

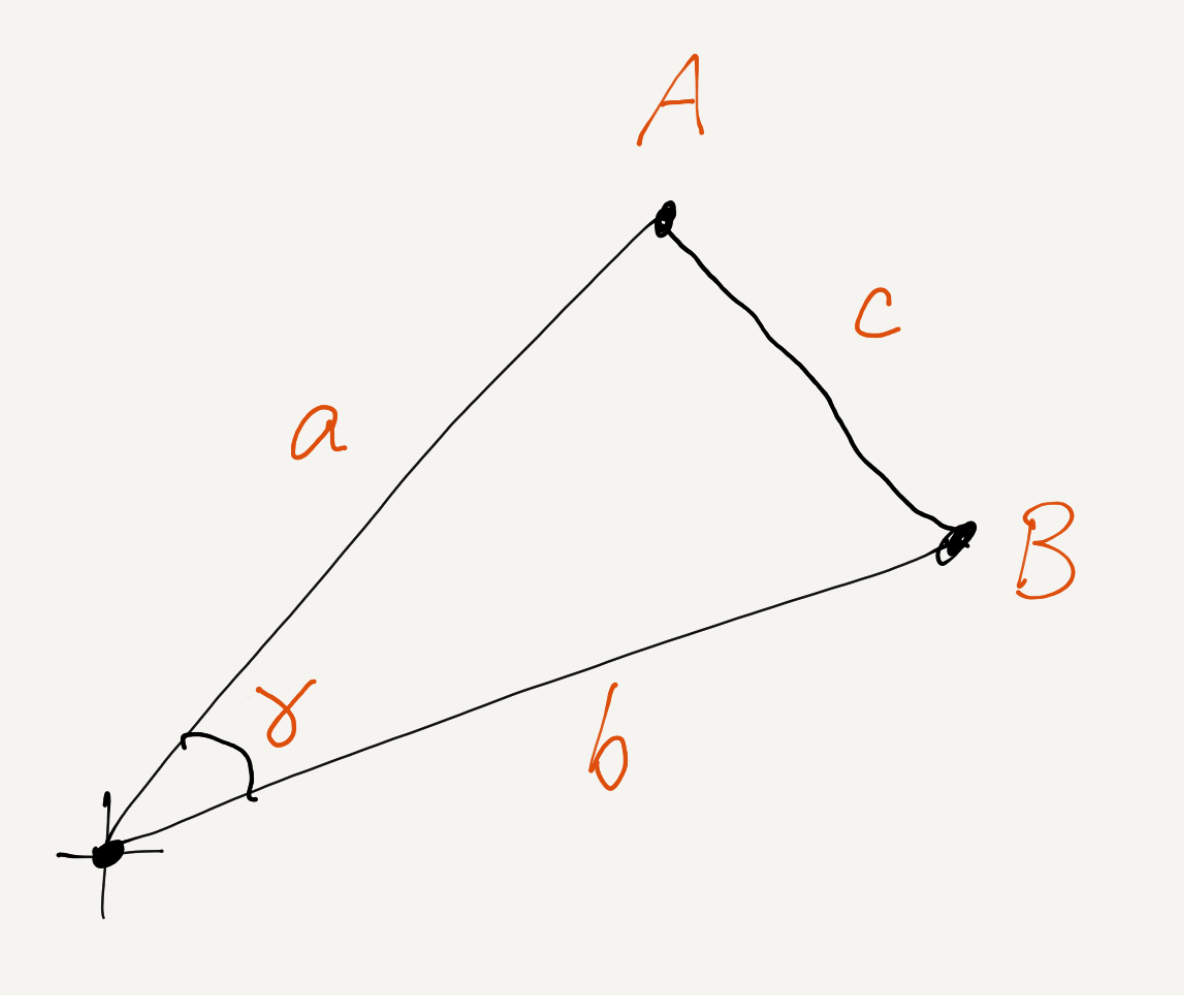
The dot product of \( A \) and \( B \) gives you the cosine of the angle \( \gamma \) between them, scaled by the product of their lengths, \( a \) and \( b \) (Equation 1). Here's a proof using the Law of Cosines.

\[ A \cdot B = \cos \left( \gamma \right) a b \tag{1} \]

Equation 1 is invoked, for example, in defining cosine similarity, often without derivation.

If, in \( n \) dimensions, the Cartesian coordinates of a point \( X \) are \( x_1, x_2, \dotso, x_n \), then the dot product \( A \cdot B \) is the sum of element-wise products as in Equation 2.

\[ A \cdot B = \sum_{i=1}^n{a_i b_i} \tag{2} \]

The dot product is so simple, it's a little surprising a nice trigonometric function like cosine should come out of it in arbitrary high-dimensional spaces.

Notation has been chosen so as to write the Law of Cosines as usual in Equation 3.

\[ c^2 = a^2 + b^2 - 2 a b \cos \left( \gamma \right) \tag{3} \]

The \( c^2 \) in Equation 3 is the square of the distance from \( A \) to \( B \) and can also be written, using the Pythagorean theorem, as in Equation 4.

\[ c^2 = \sum_{i=1}^k{ \left( a_i - b_i \right)^2 } = \sum_{i=1}^k{ a_i^2 + b_i^2 - 2 a_i b_i } = a^2 + b^2 - 2 \sum_{i=1}^k{ a_i b_i } \tag{4} \]

Equating the right hands of Equations 3 and 4, and recognizing the dot product as in Equation 2, we've built Equation 1 from scratch. \( \Box \)

It's also possible to use two-dimensional right triangle visualization thinking to see how dot product projects one vector onto another, with scaling by the lengths of the vectors. 3Blue1Brown has a great video. It's easy to connect to the usual definition of cosine.

Since you can always rotate your coordinate frame to get one vector with all zero coordinates except for one, and the other vector with all zero coordinates except for that one and one more, it's clear that dot product should give cosine in that frame, but it isn't necessarily obvious (to me) that everything works out in other coordinate frames. The proof above gives me confidence that it does. (Not that I didn't believe it before, but it's nice to have a reason.)

I wasn't quite satisfied with cosine similarity via dot product for a long time. My satisfaction now and the proof above is based quite directly on the proof Hamming generously gives on pages 117-118 of The Art of Doing Science and Engineering. As he says there (italics in original):

"I have found it very valuable in important situations to review all the basic derivations involved so I have a firm feeling for what is going on."

He uses different (possibly better?) notation, and his figure is certainly nicer than mine.