Q-Learning Tic-Tac-Toe, Briefly

Sunday November 3, 2019

Tic-tac-toe doesn't call for reinforcement learning, except as an exercise or illustration. Recently, I saw several examples implementing Q-learning, all of which were rather long. I thought I'd give tic-tac-toe with Q-learning a try myself, using Python and TensorFlow, aiming for brevity.

The board is represented with a matrix, where zero means empty.

def new_board(size):
    return np.zeros(shape=(size, size))

Moves are represented by their coordinates, like [0, 0] for the upper left.

def available_moves(board):
    return np.argwhere(board == 0)

The first player is +1 and the second player is -1, so having three in a row means getting a row, column, or diagonal to sum to +3 or -3, respectively.

def check_game_end(board):
    best = max(list(board.sum(axis=0)) +    # columns
               list(board.sum(axis=1)) +    # rows
               [board.trace()] +            # main diagonal
               [np.fliplr(board).trace()],  # other diagonal
               key=abs)
    if abs(best) == board.shape[0]:  # assumes square board
        return np.sign(best)  # winning player, +1 or -1
    if available_moves(board).size == 0:
        return 0  # a draw (otherwise, return None by default)

Q-learning will require some state, so a player will be an object with a move method that takes a board and returns the coordinates of the chosen move. Here's a random player:

class RandomPlayer(Player):
    def move(self, board):
        return random.choice(available_moves(board))

This is sufficient for the game loop, starting from any initial board:

def play(board, player_objs):
    player = +1
    game_end = check_game_end(board)
    while game_end is None:
        move = player_objs[player].move(board)
        board[tuple(move)] = player
        game_end = check_game_end(board)
        player *= -1  # switch players
    return game_end

So this plays out a game between two random players and gives the result:

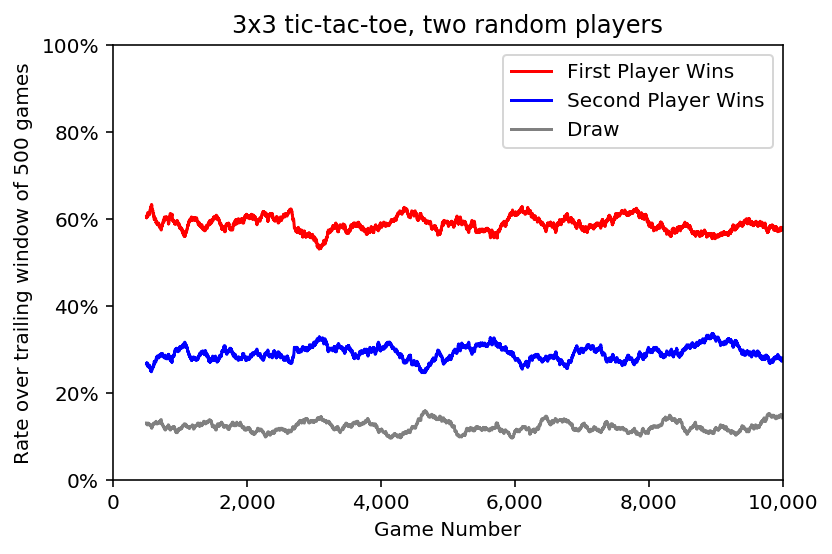
play(new_board(3), {+1: RandomPlayer(), -1: RandomPlayer()})

Playing out 10,000 games, it's clear that the first random player is more likely to win, and also that results can vary a good deal even when averaging over 500 games.

3x3 tic-tac-toe, two random players

Here's a boring player that chooses the first available move from left to right, top to bottom:

class BoringPlayer(Player):
    def move(self, board):
        return available_moves(board)[0]

Games between boring players always end the same way. The comparison with the random player is more interesting. This table give results for 10,000 games per row:

| Size | First Player | Second Player | Draw |
|------|--------------|---------------|------|
| 3x3  | Random: 59%  | Random: 29%   | 12%  |
| 3x3  | Boring: 78%  | Random: 18%   |  4%  |
| 3x3  | Random: 52%  | Boring: 44%   |  4%  |

The boring player does better than a random player whether it plays first or second. Now we have multiple "baselines." A learning agent should do better than the baselines.

The Q-learning player starts with a neural network that takes a board as input and produces an estimate of how good each move is from that position: Q-values.

class Agent(Player):
    def __init__(self, size):
        self.size = size
        self.model = tf.keras.Sequential()
        self.model.add(tf.keras.layers.Dense(size**2))
        self.model.compile(optimizer='sgd', loss='mean_squared_error')

A couple helper methods make the interface nicer for using and training the neural net. (There may be a better way of achieving this.)

    def predict_q(self, board):
        return self.model.predict(
            np.array([board.ravel()])).reshape(self.size, self.size)

    def fit_q(self, board, q_values):
        self.model.fit(
            np.array([board.ravel()]), np.array([q_values.ravel()]), verbose=0)

The Q-learning agent preserves some history, which is reset when a new game starts.

    def new_game(self):
        self.last_move = None
        self.board_history = []
        self.q_history = []

The move method uses the Q-network to choose the best available move and then calls the reward method to operationalize Q-learning's Bellman equation.

    def move(self, board):
        q_values = self.predict_q(board)
        temp_q = q_values.copy()
        temp_q[board != 0] = temp_q.min() - 1  # no illegal moves
        move = np.unravel_index(np.argmax(temp_q), board.shape)
        value = temp_q.max()
        if self.last_move is not None:
            self.reward(value)
        self.board_history.append(board.copy())
        self.q_history.append(q_values)
        self.last_move = move
        return move

The reward method trains the Q-network, updating a previous estimate of Q-values with a new estimate for the last chosen move.

    def reward(self, reward_value):
        new_q = self.q_history[-1].copy()
        new_q[self.last_move] = reward_value
        self.fit_q(self.board_history[-1], new_q)

Using a play function that resets games and delivers a reward of +1 for wins and -1 for losses and draws (see the full notebook), a Q-learning agent plays a random agent:

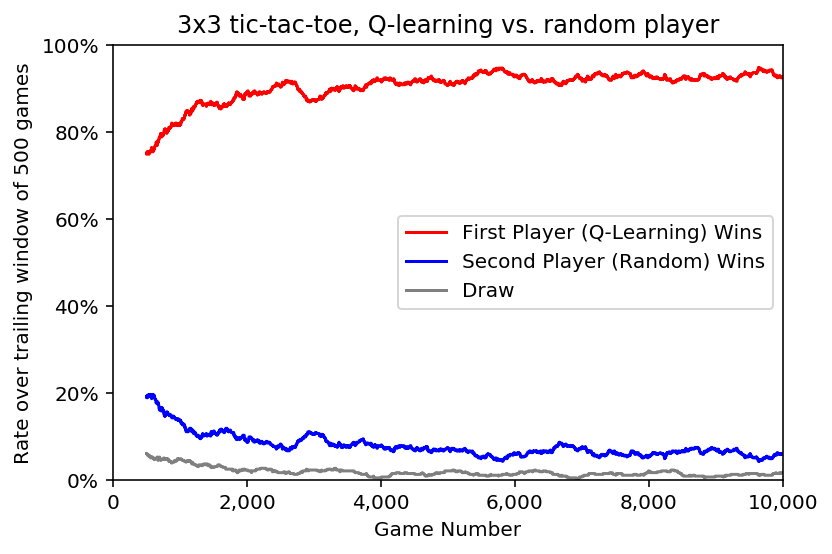
3x3 tic-tac-toe, q-learning vs. random player

The Q-learning player quickly achieves much stronger play than the baselines.

| Size | First Player | Second Player | Draw |
|------|--------------|---------------|------|
| 3x3  | Random:  59% | Random:  29%  | 12%  |
| 3x3  | Boring:  78% | Random:  18%  |  4%  |
| 3x3  | Random:  52% | Boring:  44%  |  4%  |
| 3x3  | Q-Learn: 93% | Random:   6%  |  1%  |
| 3x3  | Random:  21% | Q-Learn: 78%  |  1%  |

(For Q-learning players, they play 10,000 games while learning and then another 10,000 games while frozen to evaluate their performance level after learning, which is what's shown in the table.)

And that's it! Tic-tac-toe with a Q-learning agent, comfortably under 100 lines of code.

Ideas for doing more

| Size | First Player | Second Player | Draw |
|------|--------------|---------------|------|
| 3x3  | Random: 59%  | Random: 29%   | 12%  |
| 4x4  | Random: 31%  | Random: 27%   | 42%  |
| 5x5  | Random: 25%  | Random: 15%   | 60%  |

As the board gets bigger, the advantage of going first decreases and the probability of a draw goes up considerably.

It also takes a good deal more games to learn a good strategy:

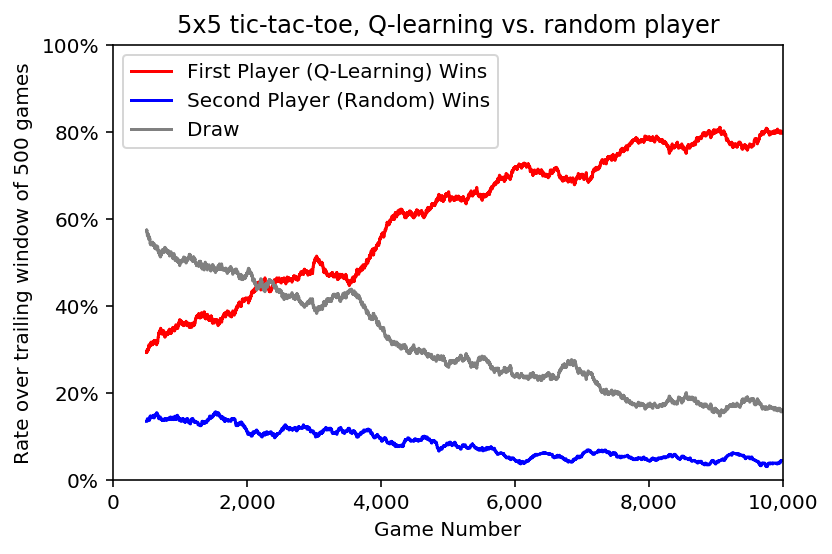
3x3 tic-tac-toe, q-learning vs. random player

For the implementations here, some results are as follows:

| Size | First Player | Second Player | Draw |
|------|--------------|---------------|------|
| 4x4  | Random:  31% | Random:  27%  | 42%  |
| 4x4  | Q-Learn: 83% | Random:  10%  |  7%  |
| 4x4  | Random:  11% | Q-Learn: 80%  |  9%  |
| 5x5  | Random:  25% | Random:  15%  | 60%  |
| 5x5  | Q-Learn: 79% | Random:   5%  | 16%  |
| 5x5  | Random:  18% | Q-Learn: 53%  | 29%  |

What is optimal for these larger boards? How well can you do? At what point is a Q-learning approach more effective (considering the trade with compute time) than exhaustive minimax search, if ever?