Finding the MIC of a circle

Tuesday February 5, 2013

Maximal Information Coefficient is a measure of two-variable dependence with some interesting properties. Full information and details on how to calculate MIC using R are available at exploredata.net. Here I calculate the MIC for an example (originally here) that Andrew Gelman posed on his blog.

This is Gelman's proposed test data, with seed set to 42 for replicability.

set.seed(42)
n <- 1000
theta <- runif(n, 0, 2 * pi)
x <- cos(theta)
y <- sin(theta)
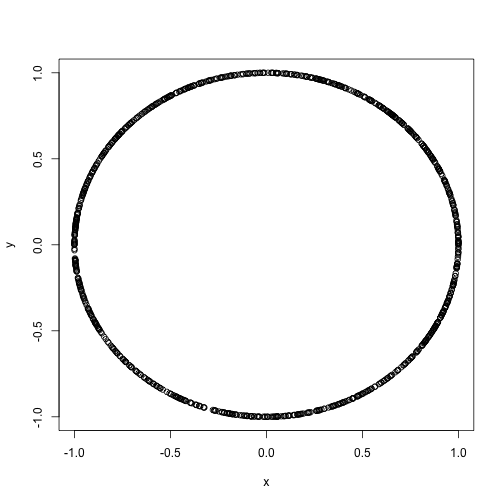
plot(x, y)

Sure enough this looks like a circle, which is clearly a relationship between x and y, but a standard correlation coefficient will not indicate this.

> cor(x, y)
## [1] -0.008817

The interface to work with MINE is a little clumsy, but this will do it. (Be sure to have the R package rJava installed.)

df <- data.frame(x, y)
write.csv(df, "data.csv", row.names = FALSE)
source("MINE.r")
MINE("data.csv", "all.pairs")

## *********************************************************
## MINE version 1.0.1d
## Copyright 2011 by David Reshef and Yakir Reshef.
##
## This application is licensed under a Creative Commons
## Attribution-NonCommercial-NoDerivs 3.0 Unported License.
## See
## http://creativecommons.org/licenses/by-nc-nd/3.0/ for
## more information.
## *********************************************************
##
##
## input file = data.csv
## analysis style = allpairs
## results file name = 'data.csv,allpairs,cv=0.0,B=n^0.6,Results.csv'
## print status frequency = every 100 variable pairs
## status file name = 'data.csv,allpairs,cv=0.0,B=n^0.6,Status.txt'
## alpha = 0.6
## numClumpsFactor = 15.0
## debug level = 0
## required common values fraction = 0.0
## garbage collection forced every 2147483647 variable pairs
## reading in dataset...
## done.
## Analyzing...
## 1 calculating: "y" vs "x"...
## 1 variable pairs analyzed.
## Sorting results in descending order...
## done. printing results
## Analysis finished. See file "data.csv,allpairs,cv=0.0,B=n^0.6,Results.csv" for output

results <- read.csv("data.csv,allpairs,cv=0.0,B=n^0.6,Results.csv")
t(results)

##                        [,1]
## X.var                  "y"
## Y.var                  "x"
## MIC..strength.         "0.6545"
## MIC.p.2..nonlinearity. "0.6544"
## MAS..non.monotonicity. "0.04643"
## MEV..functionality.    "0.3449"
## MCN..complexity.       "5.977"
## Linear.regression..p.  "-0.008817"

The result is that the MIC for this case is 0.6545, and the relation is highly non-linear. It isn't clear that 0.65 is the 'right' answer for a circle, but it does provide more indication of a relationship than a correlation coefficient of zero does.

[This post also on rPubs.]

This post was originally hosted elsewhere.